
Image A

Image B
In this project, I produced image mosaics through registering, warping, and resampling and implemented feature matching for autostiching.
This is an example of the correspondence points picked by hand for a pair of images that were used to generate a homography matrix.

Image A

Image B
To generate the homography matrix for warping the images, I solved an over-contstrained least squares problem using the correspondence points from the two images which maps the coordinate points from the space of imageB to imageA's. Then, I wrote a warp function which takes in the image and the homography matrix and finds the homogenous points in the warped space, then using the inverse of the warp matrix, warps the points back into the original image's space, and uses an interpolation function to get the pixel values from that image.
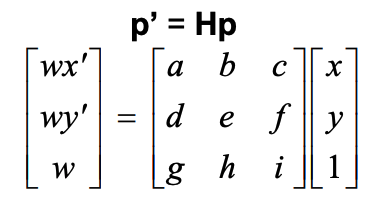
To test my homography and warping methods, I rectified images for known rectangular objects, giving a top down view of them. I took the corner points of the rectangular object in the images and warped them to coordinate points of a rectangle which causes the image to be warped as if the object was being looked at from top-down.

Image 1

Image 1 Rectified

Image 2

Image 2 Rectified
Now, to create a mosaic I first warped imageB to imageA using the method explained above which aligns the two images. Then, I created a large mosaic canvas to fit both images by placing the warped imageB onto the mosaic and blending it with imageA in the regions they overlap. To blend the images, I used a laplacian pyramid along with an alpha blending mask that transitions from 1 to 0 from the middle half of the overlapping areas. This removes the high frequency ghosting which occured when trying to blend solely with the alpha mask.

Image A

Image B

Mosaic

Image A

Image B

Mosaic

Image A

Image B

Mosaic
First, corners were automatically chosen following the harris interest point detector method for both images. This method computes a 'cornerness' value for each pixel based on a matrix multiplication of the image and a matrix involving the directional gradients, and is then thresholded to get corners.

Image A Harris Corners

Image B Harris Corners
However, as you can see, there are still too many harris corners to efficiently process. Thus, adaptive nms is implemented to reduce redunant corners. This is done by iterating over each corner, and finding the nearest corner to that corner in which the other corner has a value that is signifcantly larger than its own, which is set by x_i < c_robustness * x_j, where x_i is the current corner, x_j are all other corners, and c_robustness is set to 0.9. Then, the corners with the largest distance to another corner which meets the threshold are selected. I set the number of corners to be 500.

Image A Adaptive NMS

Image B Apdative NMS
Now, matching corners need to be filtered which is done by feature matching. First, features are extracted from each image by selecting a 40x40 patch centered around each corner, resizing it to 8x8, normalizing it by subtracting the mean and dividing by the standard deviation to account for differences in intensity, and flattening it. Then, for each feature in imageA, its error with all features in imageB are calculated. If the ratio of the two lowest errors are below a lowe threshold, which is set to 0.5, then the lowest error feature from imageB is chosen as a match for that corresponding feature in imageA. All corners still remaining are shown.

Image A Matched Features

Image B Matched Features
However, there are still some points that do not properly match across images or may not be great correspondence points. These outliers signifcantly hurt least squares problems, which is how our homography matrix is calculated, and thus another algorithm must be used to solve this. Thus, I implemented RANSAC which for n (1000) interations, randomly selects 4 points of corresopnding points and calculates an exact homography matrix and calculated the amount of inliers for that selection. Inliers were chosen as points that were warped from their corresponding points in imageB to within 1 pixel (epsilon threshold) of their matched point in imageA, which was from the previous feature matcher. Then, for the selection with the most inliers, the inliers were added to the 4 points and an over-constrained homograhphy matrix was calculated, and warping and blending was done the same as before. Side-by-side results of hand-picked correspondence to the automatic process are shown.

Inliers Selected from RANSAC

Hand-Picked Correspondence Mosaic

Automatic Mosaic

Hand-Picked Correspondence Mosaic

Automatic Mosaic

Hand-Picked Correspondence Mosaic

Automatic Mosaic
It seems as though feature matching and RANSAC leads to better results and less ghosting. This is probably because it was hard to find great points in the image that I could match up perfectly by hand, and the automatic method removed some ghosting artifacts seen in the hand-picked method. The coolest thing I learned from this project definitely everything on image warping and how to project an image into the plane of another's given that they were taken from the same center of project. I also enjoyed reading the MOPS paper and implementing the automatic feature matching and implementing RANSAC, and algorithm I have heard a lot about before but have never dived deeply into how it worked.
Following the MOPS paper, I implemented the auto stitching which is rotationally invariant. This was done by smoothening the image patch with a gaussian, finding a gradient orientation matrix by taking the arctan between the dy and dx gradients, calculating a 2D rotational matrix based on the calculated angles, and then rotating the patch using this matrix and an affine warp, then doing the same process as before from there.

Image A

Rotated Image B

Mosaic

Image A

Rotated Image B

Mosaic