
dx

dy

Gradient Magnitude

Binarized Gradient Magnitude
The first part of this project explores filter for various tasks such as image sharpening and edge detection.
To find edges in an image I convolved dx and dy filters with an input image to find changes in the vertical and horizontal directions respectively. Becuase partial derivatives can result in positive and negative values, I normalized the pixel values to be in the standard image range while showing high mangitude values to be prominent. 2D convolution works on a single channel matrix, so I tried running the filter on individual color channels, but found that converting the image to grayscale and then doing convolution worked much better. Next, I computed the gradient magnitude image which effectively combines the two partial derivatives by taking the square root of the sum of the two partial derivatives squared. Lastly, to make the edges clearer and reduce noise, I binarized the gardient mangitude by thresholding the image so any values below the threshold would be set to 0, and anything above would be 1. This causes pixels with a higher value, indiciating higher change, to be set to white.

dx

dy

Gradient Magnitude

Binarized Gradient Magnitude
However, as you can see, the edge detection with gradients on the original image results in noisy outputs. To prevent this, I passed the image through a low pass filter by convolving it with a gaussian blur kernel. The gaussian kernerl smooths an image by interpolating nearby values with weights given by a gaussian curve. Then, I convovled that output with the partial derivative filters above and did the same process. I found these images to have thicker edges and signifcantly less nosie due to the smoothening affect. Because convolution is an associative and commutative operation, we can combine the blurring and edge detection process into a single convolution by first convolving the gaussian kernel with the partial derivative filters, and then convolving the new filter onto the image, which gives the exact same results.

dx

dy

Gradient Magnitude

Binarized Gradient Magnitude
Filters can also allow us to sharpen images. To do so, the image is passed through a low pass filter, such as the same gaussian kernel before, and then the output is subtracted from the original image. This results in an image with only high frequencies, as the low frequences given by the low pass filter were subtracted. Then, the high frequencies are added back to the original image with a scaling facter α, resulting in the image looking sharper. To show the effectiveness of this process, a high quality image was blurred using a gaussian kernel and then resharpened.

Taj Mahal

Sharpened Taj Mahal

Original Photo

Sharpened Image

Sharp HQ Image

Blurred Version

Sharpened Version (Blurred)
Hybrid images can be formed by passing two images through high and low pass filters and then averaging them. The image that undergoes a high pass transformation will be seen close up by the human eye, while the image passed through a low pass filter can be seen from much further away. We can see the result of this process by analyzing the image in the frequency domain through a Fourier transform. The Fourier analysis done at the end is for the last set of images. I also included a failure at the end where the frequencies were not able to be distinguished well.

Image 1

Image 2

Hybrid

Image 1

Image 2

Hybrid

Image 1

Image 2

Hybrid
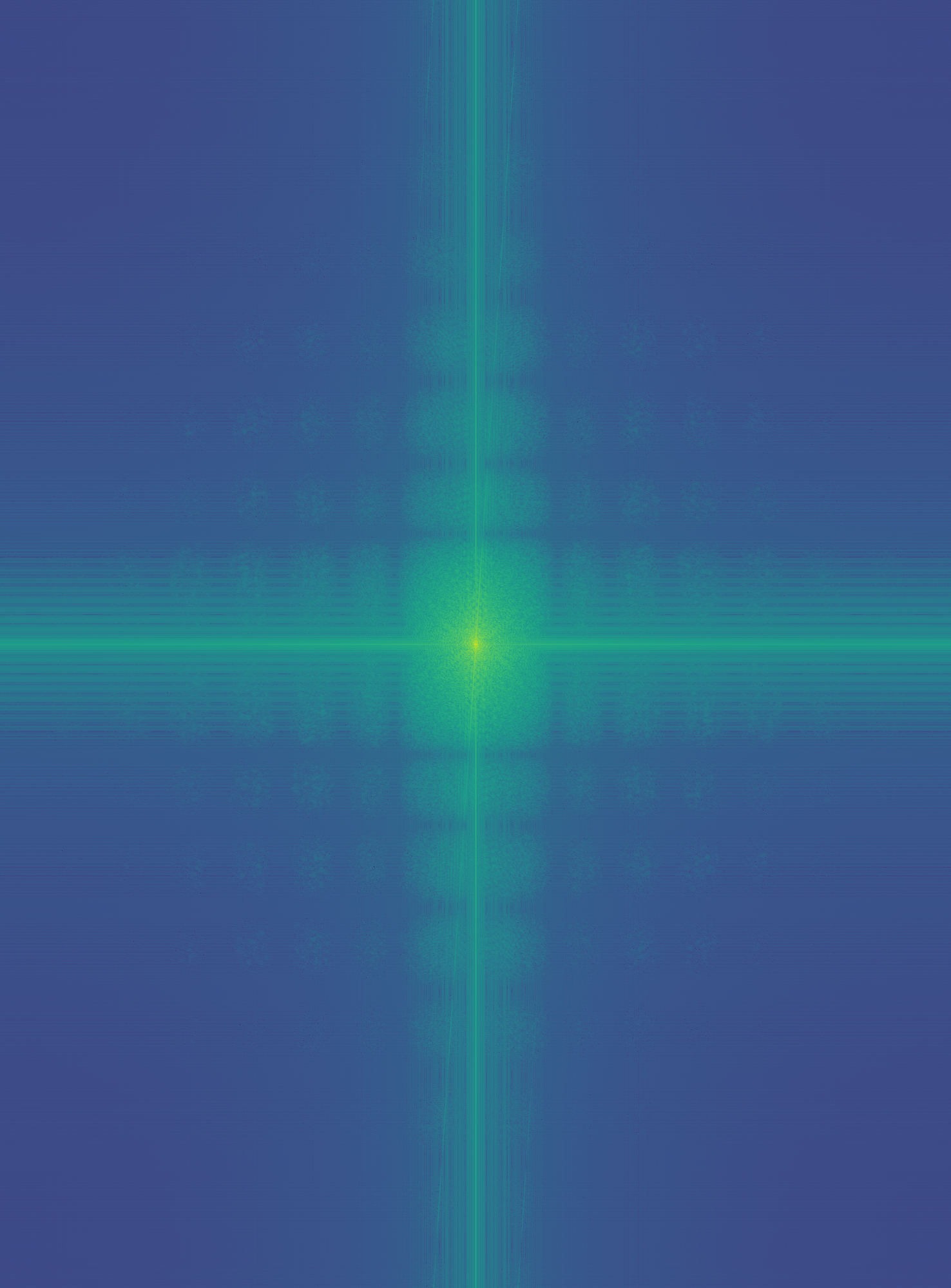
Low-pass Fourier

High-pass Fourier

Hybrid Fourier

Tiger

Lion

Failed Hybrid
To effectively blend two images, gaussian and laplacian stacks help through the blending of images at various resolutions. I first construct a gaussian stack which simply keeps an image the same spatial dimensions but progressively applies a gaussian kernel to blur it at multiple levels. The laplacian stack of an image is calculated by subtracting the next image in the guassian stack from the current level in the gaussian stack, and using the last image in the gaussian stack as the last in the laplacian. The first row is the apple laplacian stack, the second is the orange, and third is combined with the mask.

Level 0

Level 2

Level 4

Level 0

Level 2

Level 4

Level 0

Level 2

Level 4
With the code from the previous section, we can now easily blend images by simply adding all the images in the stack from the mask and the laplacian stacks of the two images. With a gaussian stack of the mask, I multiply the mask by the first image, and multiply the opposing mask to the second image at each layer, and then sum across all the images.

Apple

Orange

Oraple

Sunset

Beach

Mask

Result

Moon

Skyline

Mask

Result

Moon Laplacian Stack

Moon Laplacian Stack
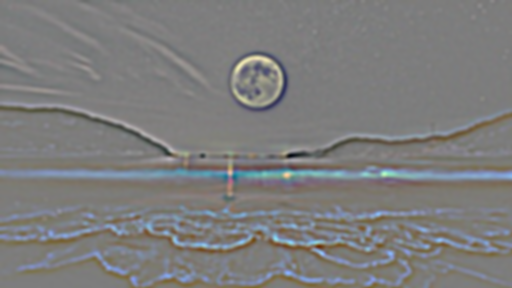
Moon Laplacian Stack

Moon Laplacian Stack

Moon Laplacian Stack

Skyline Laplacian Stack

Skyline Laplacian Stack

Skyline Laplacian Stack

Skyline Laplacian Stack

Skyline Laplacian Stack

Combined Laplacian Stack

Combined Laplacian Stack

Combined Laplacian Stack

Combined Laplacian Stack

Combined Laplacian Stack
Did multi-resolution blending in color